Written by xi-jjun
on April 15, 2021

컴퓨터 구조 - 4

컴퓨터 구조 4강

KOCW 컴퓨터구조 2020-2학기 최규상 교수님 강의를 듣고 정리한 글이다.

Six Step in Execution of a Procedure

Main routine(Caller)가 procedure(Callee)가 접근할 수 있는 곳에 argument를 넣는다.

→ $a0 ~ $a3
Caller가 Callee에게 제어를 넘긴다.
Callee가 필요한 메모리 공간(Stack)을 할당 받는다.
Callee의 코드를 실행.
실행의 결과값을 result register에 저장. → $v0, $v1
return address register 에 있던 주소를 반환해서 다음 코드를 진행해준다. → $ra

이렇게 글로만 적어놓으면 이해가 잘 안간다. 따라서 간단한 예시 코드를 작성하여 비교해보겠다.

#include <stdio.h>

int sum(int x, int y) {
  return x + y;
}

int main(){ 
  int a = 1, b = 2;
  int result;
  
  result = sum(a, b); 
  // 1. Caller(main)이 Callee(sum) 호출.
  // 2. argument 1, 2 가 $a0, $a1로 전달된다.
  // 3. Callee(sum)가 메모리 할당 받고, 해당 기능(sum) 실행.
  // 4. 결과를 $v0에 저장. → 3
  // 5. $ra에 다음 코드의 명령어 주소가 저장돼있다. 
  
  printf("%d", result); // 6. $ra에 저장된 주소로 반환된 후 Callee(sum) 이후의 코드가 진행된다.
  
  return 0;
}

현재 위 주석의 설명만 봐서는 의문이 드는 것이 많을 수 있다. 이후에 더 자세히 나올 예정이니 이렇게 흘러간다는 것만 알고 넘어갈 것이다.

Procedure Call Instructions

MIPS assembly language는 register를 할당할 뿐 아니 procedure를 위한 명령어도 제공한다.

# jal(jump-and-link instruction) → procedure call
jal ProcedureLabel # 이 다음에 올 명령어는 ProcedureLabel이 있는 명령어이다. 동시에 다음에 올 명령어 주소를 $ra에 저장한다.

# 예시 코드 1 → 2 → 3 순서로 진행
jal LabelA # 1. LabelA의 주소를 pc에 넣는다. 동시에 다음에 올 명령어(add) 주소를 $ra에 넣는다.
add $t0, $t1, $zero # 3. LabelA의 루틴이 끝나면 $ra에 저장돼있는 주소로 돌아와서 코드를 다시 진행시킨다.
...
LabelA : # 2. 해당 루틴 실행
	...

# jr(jump register) → procedure return
jr $ra # $ra값을 pc에 복사. Callee가 Caller에게 제어를 넘긴다.

jr $ra 는 $ra에 저장되어 있는 주소로 jump하라는 뜻이다. Caller는 $a0~$a3에 전달할 argument값을 넣은 후 jal X명령을 이용해서 procedure X(Callee)로 jump한다. Callee는 본인의 루틴을 끝낸 후 결과를 $v0~$v1에 넣은 후 jr $ra명령을 실행하여 복귀한다. 자 이제 아까 위에서의 C코드를 다시 살펴보겠다.

#include <stdio.h>

int sum(int x, int y) {
  return x + y;
}

int main(){ 
  int a = 1, b = 2;
  int result;
  
  result = sum(a, b); 
  // 1. jal LabelSum 으로 $ra=printf코드 명령어주소 저장. LabelSum procedure(Callee:sum) 호출.
  // 2. argument 1, 2 가 $a0, $a1로 전달된다.
  // 3. Callee(sum)가 메모리 할당 받고, 해당 기능(sum) 실행.
  // 4. 결과를 $v0에 저장. → 3
  // 5. $ra에 다음 코드의 명령어 주소가 저장돼있다. → 1번 수행 때문에 저장된 것.
  
  printf("%d", result); // 6. $ra에 저장된 주소로 반환된 후 Callee(sum) 이후의 코드가 진행된다.
  
  return 0;
}

이정도로 설명할 수 있을 것 같다.

Leaf Procedure Example

Leaf Procedure : 1개의 procedure에서 다른 procedure를 부르지 않는 것.

int leaf_example(int g, int h, int i, int j) {
  int f;
  f = (g + h) - (i + j);
  return f;
}

위 C코드를 MIPS assembly 코드로 바꿔보겠다.

Argument g, h, i, j는 $a0 ~ $a3에 해당. f는 $s0에 해당한다. 컴파일된 프로그램은 procedure label로부터 시작된다.

# main..
...
jal leaf_example # $ra=다른 어떤 main의 코드 주소. leaf_example 라벨로 pc에 넣어준다.
다른 어떤 main의 코드..
...

# procedure..
leaf_example: # main routine의 jal에 의해 leaf_example() 호출됨.
  addi $sp, $sp, -4 # int f라는 지역변수를 설정. stack의 공간을 4byte 할당해준다.
  sw $s0, 0($sp) # 우리는 f를 $s0에 저장할 것이기 때문에 원래 $s0에 있던 값을 stack에 저장.

  add $t0, $a0, $a1 # g + h
  add $t1, $a2, $a3 # i + j
  sub $s0, $t0, $t1 # f = (g + h) - (i + j)
  add $v0, $s0, $zero # 결과값을 result register에 저장. $s0더이상 필요없음.

  lw $s0, 0($sp) # stack에 있던 원래 $s0값을 다시 $s0에 복사해준다.
  add $sp, $sp, 4 # 할당해줬던 4byte를 다시 해제.
  jr $ra # $ra를 pc에 넣어준다. "다른 어떤 main의 코드.." 로 간다.

여기서 의문이 들었던 점은 왜 $t0, $t1register들은 stack에 저장을 안해주는가? 였다. 책에서는 다음과 같이 설명돼있었다.

사용하지도 않는 register값을 쓸데없이 저장했다 복구하는 일이 생길 수 있다. 특히 임시 register에 대해 이런 일이 발행할 가능성이 크다. 이를 예방하기 위해 MIPS 소프트웨어는 register 18개를 2 종류로 나눈다.

$t0 ~ $t9 : procedure 호출 시 Callee가 값을 보존해 주지 않는 임시 register.

$s0 ~ $s7 : procedure 호출 전과 후의 값이 같게 유지되어야 하는 변수 register 8개. (Callee는 이 register 사용하게 되면 원래 값을 저장했다가 원상 복구해야한다.)

간단하게 MIPS에서 procedure 호출에 따른 stack 을 그림으로 봐보자.

ca4_1

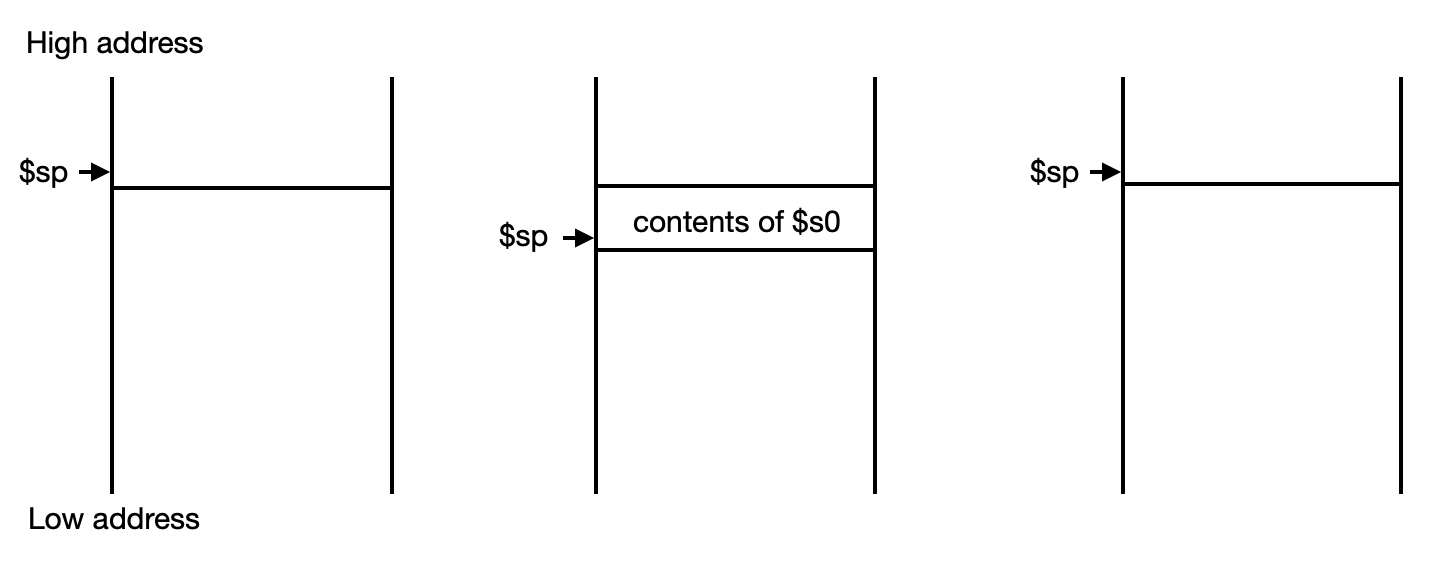
contents of $s0 : $s0의 값.
$sp : stack pointer

Non-Leaf Procedure Example

세상의 모든 procedure가 leaf procedure라면 매우 간단할 것이다. 그러나 그렇지 않다. 예를 들면 procedure안에서 다른 procedure를 호출하고, 그 호출된 procedure에서 또 다른 procedure를 호출한다면… 심지어 각각 호출된 procedure가 모두 argument를 가질 때 $a0은 계속 overwritten될 것이다. 이런 충돌을 방지하기 위한 한가지 방법으로 값이 보존돼야 할 모든 register를 stack에 넣는 것이다. $sp는 stack에 저장되는 register 개수에 맞춰서 조정된다. procedure가 return한 후에는 메모리에서 다시 값을 꺼내 register를 원상복구하고 이에 맞춰서 $sp를 다시 조정한다.

글로만 장황하게 쓰면 또 이해가 완벽히 안될 수 있기에 책에 나오는 factorial(recursive procedure) procedure를 MIPS assembly code로 바꿔보겠다.

// Non-leaf Procedure example
int factorial(int n) {
  if(n < 1) return 1;
  else return n * factorial(n-1);
}

# main
...
jal factorial # factorial로 점프.
...
# factorial procedure
factorial:
  addi $sp, $sp, -8 # stack에 공간 할당. $ra, $a0를 저장하기 위함.
  sw $ra, 4($sp) # $ra값이 stack에 추가됨.
  sw $a0, 0($sp) # $a0값이 stack에 추가됨.
	
  # if(n < 1)+else 판단하는 코드
  slti $t0, $a0, 1 # n<1이면 $t0=1, n>=1이면 $t0=0
  beq $t0, $zero, L1 # n>=1이면 $t0=0라고 위 코드에서 명시함. ($t0=0)==$zero 같으므로 L1으로 점프.
  
  # if(n < 1)인 경우
  addi $v0, $zero, 1 # return 1
  addi $sp, $sp, 8 # stack에 할당했던 공간 해제.
  jr $ra # return to the Caller
  
  # else인 경우
L1:
  addi $a0, $a0, -1 # n - 1
  jal factorial # call factorial(n - 1) recursive start!!

  # when recursive end
  lw $a0, 0($sp) # argument n restore
  lw $ra, 4($sp) # return address 복구
  addi $sp, $sp, 8 # recursive끝나고 왔으니 끝난 procedure의 stack 공간 해제

  # n * factorial(n - 1)
  mul $v0, $a0, $v0 # return n * factorial(n - 1)
  jr $ra # return to the Caller

위와 같이 정리할 수 있다. 완벽한 이해를 위해 해당코드에 n=2을 넣고 직접 과정을 그려가볼 것이다. 그 전에 한가지를 더 알고 가보자.

Local Data on the Stack

$sp : 현재 stack의 top값을 가리키고 있다.
procedure frame : 함수를 실행하면 그 함수를 위한 frame이 만들어진다. activation record라고도 부른다.
$fp : MIPS 소프트웨어 중에는 frame pointer가 procedure frame의 첫번째 word를 가리키도록 하는 것이 있다.

자 이제 $fp의 존재를 알게 되었다. stack에 점점 register값이 쌓이게 되면 procedure 내에서 $sp값이 변하는 경우가 생길 때 지역변수 참조가 어려워진다. 그러나 $fp를 사용하게 되면 변하지 않는 base register역할을 하기 때문에 지역변수 참조가 간단해진다.

Factorial(2) 실제로 계산해보기

$fp를 사용하려면 $sp값을 $fp으로 원상 복구해야 하는데 지금은 그렇게 안하고 $fp가 가리키는 곳을 나타내기만 해보겠다. 어셈블리 코드 내에서는 주석으로 명시해놓을 것이다. 그리고 아래의 어셈블리 코드들은 예시 argument에 맞게 실행되는 순서를 나타낸 것이다.

// Non-leaf Procedure example. if n = 2
int factorial(int n) { // n = 2 
  if(n < 1) return 1;
  else return n * factorial(n-1);
}

ca4_2

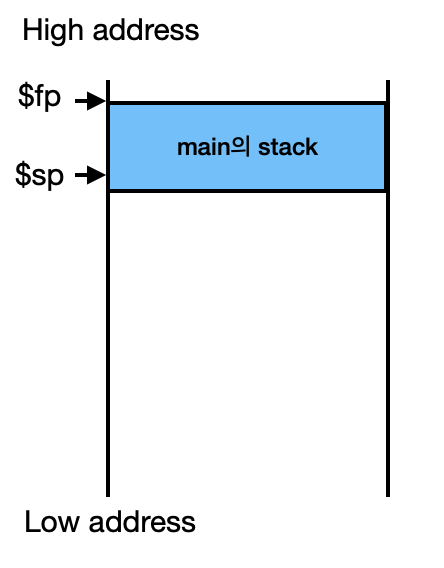
Factorial( int n )이 호출되기 바로 직전 Stack의 상태이다. $sp는 당연히 stack의 top을 가리키고 있고, $fp는 base register 역할을 하고 있다.

# main
...
jal factorial # factorial로 점프. factorial(2) $a0=2, $ra="main의 다음코드 주소"
main의 다음코드
...
# factorial procedure
factorial:
  addi $sp, $sp, -8 # stack에 공간 할당. $ra, $a0를 저장하기 위함.
  sw $ra, 4($sp) # $ra="main의 다음코드 주소값"이 stack에 추가됨.
  sw $a0, 0($sp) # $a0=2 값이 stack에 추가됨.

ca4_3

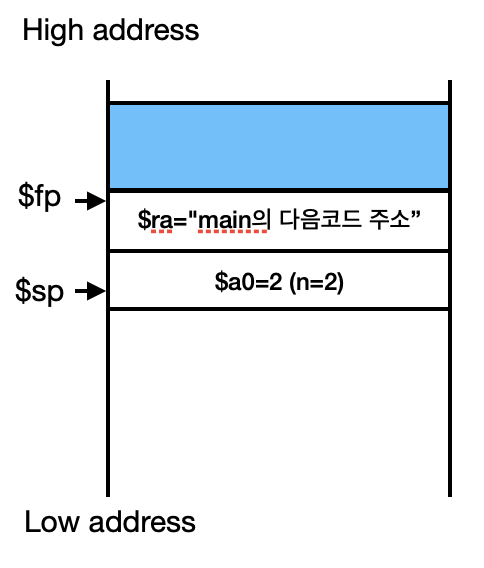
Factorial(Callee)에서 $a0, $ra register를 사용할 것이기 때문에 main과 충돌방지를 위해서 main에서 쓰던 값들을 stack에 안전하게 저장해 준다.

  # if, else 판단하는 코드
  slti $t0, $a0, 1 # $a0=2이므로 $a0>1이다. 따라서 $t0=0
  beq $t0, $zero, L1 # $t0=0라고 위 코드에서 명시함. ($t0=0)==$zero 같으므로 L1(else)으로 점프.

  # else인 경우
L1:
  addi $a0, $a0, -1 # $a0=1 이 된다. *이미 $a0=2는 stack에 저장된 상태.
  jal factorial # call factorial(1) recursive1 start!! $ra="lw $a0, 0($sp) <-fact"가 된다.
  # lw $a0, 0($sp) <-fact : factorial 첫 호출 후 처음 recursive 호출했을 때 그 다음의 코드
  # 이전의 $ra="main의 다음코드 주소값"은 이미 stack에 잘 저장된 상태.
	
  recursive1 factorial:
    # $fp값을 $sp로 설정. 그 후 아래 실행.
    addi $sp, $sp, -8 # stack에 공간 할당. $ra, $a0를 저장하기 위함.
    sw $ra, 4($sp) # $ra="lw $a0, 0($sp) <-fact"이 stack에 추가됨.
    sw $a0, 0($sp) # $a0=1 값이 stack에 추가됨.

ca4_4

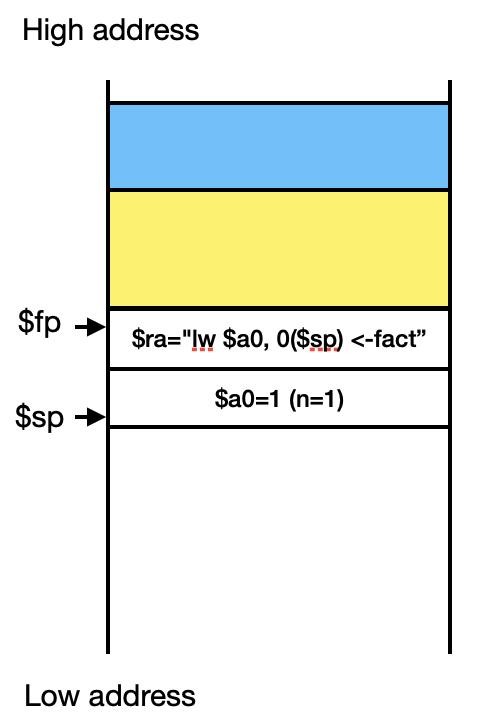
$ra="main의 다음코드 주소값"이었지만 jal에 의해서 $ra="lw $a0, 0($sp) <-fact"로 덮어씌워진다. 그러나 충돌이 방지되는 이유는 $ra="main의 다음코드 주소값"의 값은 이미 stack에 저장돼있기 때문에 Callee가 반환될 때 복구된다.

마찬가지로 addi $a0, $a0, -1에서 $a0의 값이 덮어쓰기 되지만 괜찮다. $a0=2는 이미 stack에 저장돼있기 때문이다.

그 후, recursive1 factorial:이후에 현재 $a0, $ra의 값을 stack에 넣어주게 된다. 그림은 위 과정들이 끝난 후의 시점에서의 stack이다.

    # n=1이 인자로 들어옴. n < 1이 아니므로 L1으로 점프
  recursive1 L1:
    addi $a0, $a0, -1 # $a0=0 이 된다. *이미 $a0=1은 stack에 저장된 상태.
    jal factorial # call factorial(0) recursive2 start!! $ra="lw $a0, 0($sp) <-1"가 된다.
    # lw $a0, 0($sp) <-1 : factorial 첫 호출 후 처음 호출된 recursive procedure의 다음 코드
    # 이전의 $ra="lw $a0, 0($sp) -fact"은 stack에 잘 저장된 상태.
		
    recursive2 factorial:
      # $fp값을 $sp로 설정. 그 후 아래 실행.
      addi $sp, $sp, -8 # stack에 공간 할당. $ra, $a0를 저장하기 위함.
      sw $ra, 4($sp) # $ra="lw $a0, 0($sp) <-1"이 stack에 추가됨.
      sw $a0, 0($sp) # $a0=0 값이 stack에 추가됨.

ca4_5

$ra="lw $a0, 0($sp) <-fact"이었지만 jal에 의해서 $ra="lw $a0, 0($sp) <-1"로 덮어씌워진다. 그러나 충돌이 방지되는 이유는 $ra="lw $a0, 0($sp) <-fact"의 값은 이미 stack에 저장돼있기 때문에 Callee가 반환될 때 복구된다.

마찬가지로 addi $a0, $a0, -1에서 $a0의 값이 덮어쓰기 되지만 괜찮다. $a0=1는 이미 stack에 저장돼있기 때문이다.

그 후, recursive2 factorial:이후에 현재 $a0, $ra의 값을 stack에 넣어주게 된다. 그림은 위 과정들이 끝난 후의 시점에서의 stack이다.

      # n=0이 인자로 들어옴. n < 1 만족. if문 실행.
      addi $v0, $zero, 1 # $v0=1 : return 1
      addi $sp, $sp, 8 # stack에 할당했던 공간 해제.
      jr $ra # return to "lw $a0, 0($sp) <-1"
			
      # ...recursive2 End

ca4_4

n=0이라서 else가 아닌 if조건을 실행하게 된다. $v0register에 결과값을 저장하고 할당했던 stack공간을 해제 시켜준다. 위 그림은 할당해제된 stack의 그림이다.

$ra="lw $a0, 0($sp) <-1"에서 바뀌지 않았으므로 jr명령어 때 해당 register $ra에 담긴 값으로 return. recursive2는 끝나게 된다.

    # recursive1 L1 다시 진행. - lw $a0, 0($sp) 부터
    lw $a0, 0($sp) # 0($sp)=1 를 $a0으로 복구 => $a0=1
    lw $ra, 4($sp) # return address "lw $a0, 0($sp) - fact" 복구
    addi $sp, $sp, 8 # recursive끝나고 왔으니 끝난 procedure의 stack 공간 해제
    # $fp값은 $sp값으로 설정.

ca4_3

stack에 recursive2의 메모리를 해제시켰다. stack구조는 (First In Last Out)이므로 $sp는 다시 recursive1의 top을 가리킬 것이다. recursive2의 procedure는 끝이 났으므로 recursive1에서 썼던 register($a0, $ra)를 다시 복구시켜야 한다. 그 후 recursive1이 반환되기 전에 recursive1이 썼던stack 영역 해제.

    # 1 * factorial(0)
    mul $v0, $a0, $v0 # $v0=$a0 x factorial(0)을 구해야한다. $a0=1, factorial(0)=$v0=1임을 알고 있기에 $v0=1이 된다.
    jr $ra # return to "lw $a0, 0($sp) <-fact"
		
    # ...recursive1 End

  # factorial L1 다시 진행. - lw $a0, 0($sp) 부터
  lw $a0, 0($sp) # 0($sp)=1 를 $a0으로 복구 => $a0=2
  lw $ra, 4($sp) # return address "main의 다음코드 주소값" 복구
  addi $sp, $sp, 8 # recursive끝나고 왔으니 끝난 procedure의 stack 공간 해제
  # $fp값은 $sp값으로 설정.

ca4_2

recursive1의 결과값을 결과 register에 저장. 그 후 $ra로 복귀.

처음에 호출됐던 factorial의 else조건을 이어서 진행한다. stack에서 register값 복구한 뒤에 factorial이 반환되기 전 stack 영역 해제.

  # 2 * factorial(1)
  mul $v0, $a0, $v0 # $v0=$a0 x factorial(1)을 구해야한다. $a0=2, factorial(1)=$v0=1임을 알고 있기에 $v0=2가 된다.
  jr $ra # return to "main의 다음코드 주소값"

# ...factorial(2) End

main의 다음 코드 # $ra="main의 다음코드 주소값" 이므로 factorial(n) 다음 코드 실행하는 것.
...

$v0 에 저장돼있던 값과 argument값 곱해서 다시 결과 register에 저장. 그 후 factorial procedure가 끝나고 그 다음 main의 코드 실행.

아래는 위 코드를 통합하여 코드가 실행되는 순서를 한눈에 볼 수 있게 했다.

## total ##

# main
...
jal factorial # factorial로 점프. factorial(2) $a0=2, $ra="main의 다음코드 주소"
main의 다음코드
...
# factorial procedure
factorial:
	addi $sp, $sp, -8 # stack에 공간 할당. $ra, $a0를 저장하기 위함.
	sw $ra, 4($sp) # $ra="main의 다음코드 주소값"이 stack에 추가됨.
	sw $a0, 0($sp) # $a0=2 값이 stack에 추가됨.

	# if, else 판단하는 코드
	slti $t0, $a0, 1 # $a0=2이므로 $a0>1이다. 따라서 $t0=0
	beq $t0, $zero, L1 # $t0=0라고 위 코드에서 명시함. ($t0=0)==$zero 같으므로 L1(else)으로 점프.

	# else인 경우
L1:
	addi $a0, $a0, -1 # $a0=1 이 된다. *이미 $a0=2는 stack에 저장된 상태.
	jal factorial # call factorial(1) recursive1 start!! $ra="lw $a0, 0($sp) <-fact"가 된다.
	# lw $a0, 0($sp) <-fact : factorial 첫 호출 후 처음 recursive 호출했을 때 그 다음의 코드
	# 이전의 $ra="main의 다음코드 주소값"은 이미 stack에 잘 저장된 상태.
	
	recursive1 factorial:
		# $fp값을 $sp로 설정. 그 후 아래 실행.
		addi $sp, $sp, -8 # stack에 공간 할당. $ra, $a0를 저장하기 위함.
		sw $ra, 4($sp) # $ra="lw $a0, 0($sp) <-fact"이 stack에 추가됨.
		sw $a0, 0($sp) # $a0=1 값이 stack에 추가됨.
	
	
	  # n=1이 인자로 들어옴. n < 1이 아니므로 L1으로 점프
	recursive1 L1:
		addi $a0, $a0, -1 # $a0=0 이 된다. *이미 $a0=1은 stack에 저장된 상태.
		jal factorial # call factorial(0) recursive2 start!! $ra="lw $a0, 0($sp) <-1"가 된다.
		# lw $a0, 0($sp) <-1 : factorial 첫 호출 후 처음 호출된 recursive procedure의 다음 코드
		# 이전의 $ra="lw $a0, 0($sp) -fact"은 stack에 잘 저장된 상태.
		
		recursive2 factorial:
			# $fp값을 $sp로 설정. 그 후 아래 실행.
			addi $sp, $sp, -8 # stack에 공간 할당. $ra, $a0를 저장하기 위함.
			sw $ra, 4($sp) # $ra="lw $a0, 0($sp) <-1"이 stack에 추가됨.
			sw $a0, 0($sp) # $a0=0 값이 stack에 추가됨.

			# n=0이 인자로 들어옴. n < 1 만족. if문 실행.
			addi $v0, $zero, 1 # $v0=1 : return 1
			addi $sp, $sp, 8 # stack에 할당했던 공간 해제.
			jr $ra # return to "lw $a0, 0($sp) <-1"
			
			# ...recursive2 End

		# recursive1 L1 다시 진행. - lw $a0, 0($sp) 부터
		lw $a0, 0($sp) # 0($sp)=1 를 $a0으로 복구 => $a0=1
		lw $ra, 4($sp) # return address "lw $a0, 0($sp) - fact" 복구
		addi $sp, $sp, 8 # recursive끝나고 왔으니 끝난 procedure의 stack 공간 해제
		# $fp값은 $sp값으로 설정.


		# 1 * factorial(0)
		mul $v0, $a0, $v0 # $v0=$a0 x factorial(0)을 구해야한다. $a0=1, factorial(0)=$v0=1임을 알고 있기에 $v0=1이 된다.
		jr $ra # return to "lw $a0, 0($sp) <-fact"
		
		# ...recursive1 End

	# factorial L1 다시 진행. - lw $a0, 0($sp) 부터
	lw $a0, 0($sp) # 0($sp)=1 를 $a0으로 복구 => $a0=2
	lw $ra, 4($sp) # return address "main의 다음코드 주소값" 복구
	addi $sp, $sp, 8 # recursive끝나고 왔으니 끝난 procedure의 stack 공간 해제
	# $fp값은 $sp값으로 설정.


	# 2 * factorial(1)
	mul $v0, $a0, $v0 # $v0=$a0 x factorial(1)을 구해야한다. $a0=2, factorial(1)=$v0=1임을 알고 있기에 $v0=2가 된다.
	jr $ra # return to "main의 다음코드 주소값"

# ...factorial(2) End

main의 다음 코드 # $ra="main의 다음코드 주소값" 이므로 factorial(n) 다음 코드 실행하는 것.
...

자세히 공부하려다 보니 많이 장황해진 것 같다. 자세한 설명을 예시를 들어서 보고 싶은 사람들에게는 좋을 것 같지만 한눈에 알아보기가 어렵게 썼다는게 고쳐야할 점인 것 같다.

코드에서는 $fp를 정하는 코드를 따로 안넣었습니다. 주석으로만 썼고, 그림을 좀 더 쉽게 그리기 위해서 도입했습니다. 책에서는

호출할 때의 $sp값으로 $fp를 초기화하고 나중에 $fp로 $sp를 원상 복구한다.

라고 했습니다.

Memory Layout

ca4_6

_{사진 출처}

Text : program code. Instructions.
Static Data : global variables(C의 전역변수가 저장되는 곳 $gp가 현재 static data의 위치를 가리키고 있다. 상수와 기타 정적 변수들이 들어간다. 배열의 경우 그 크기가 고정되어 있어서 정적 데이터 segment에 잘 맞는다.
Dynamic Data : Heap. 위쪽으로 자란다. C경우 malloc, Java경우 new. Linked list같은 늘어났다 줄어들었다를 반복하는 자료구조를 위한 segment를 전통적으로 Heap이라고 불러 왔다.
Stack : 아래쪽으로 자란다. Heap과 마주보며 자라도록 할당하기 때문에 메모리를 더욱 효율적으로 사용한다.

Character Data

Byte-encoded character sets
- ASCII
- Latin-1
Unicode: 32-bit character set : 전세계의 언어를 하나의 character set으로 표현
- Used in Java, C++…
- Most of the world’s alphabets +symbols
- UTF-8, UTF-16: variable-length encodings.

Byte/Halfword Operations

lb rt, offset(rs) # load byte : offsets에서 한 byte를 읽어서 rt에 넣는다.
lbu rt, offset(rs) # load byte unsigned
sb rt, offset(rs) # store byte 

lh rt, offset(rs) # load halfword
lhu rt, offset(rs) # load halfword unsigned
sh rt, offset(rs) # store halfword

32-bit Constants

대부분의 경우 상수가 작아서 16bit로 상수를 표현하기엔 충분하다. 그러나 때때로는 32bit가 필요할 수도 있다. → lui사용.

lui rt, costant # constant 값을 rt의 상위 16bit에 넣는다. 동시에 하위 16bit를 0으로 만든다.

# 2개의 명령어를 사용하여 32bit 상수를 만들 수 있다.
lui $s0, 61(decimal)
ori $s0, $s0, 2304(decimal)

위처럼 안하게 된다면, 메모리에서 32bit 상수값을 load해야 한다. 따라서 1개의 명령어만 있으면 되지만 성능적인 측면에서 위 코드가 훨씬 더 좋다. 왜냐하면 memory access 가 더 느리기 때문이다.

Branch Far Away

Branch target이 16bit offset으로 표현하기에 너무 멀다면, assembler는 code를 rewrite한다.

beq $s0, $s1, L1 # L1이 너무 멀다면 아래와 같이 rewrite한다.

bne $s0, $s1, L2 
j L1 # j는 offset으로 26bit까지 사용가능. 따라서 더 멀리까지 표현 가능.

Addressing Mode Summary

ca4_7

_{사진 출처}

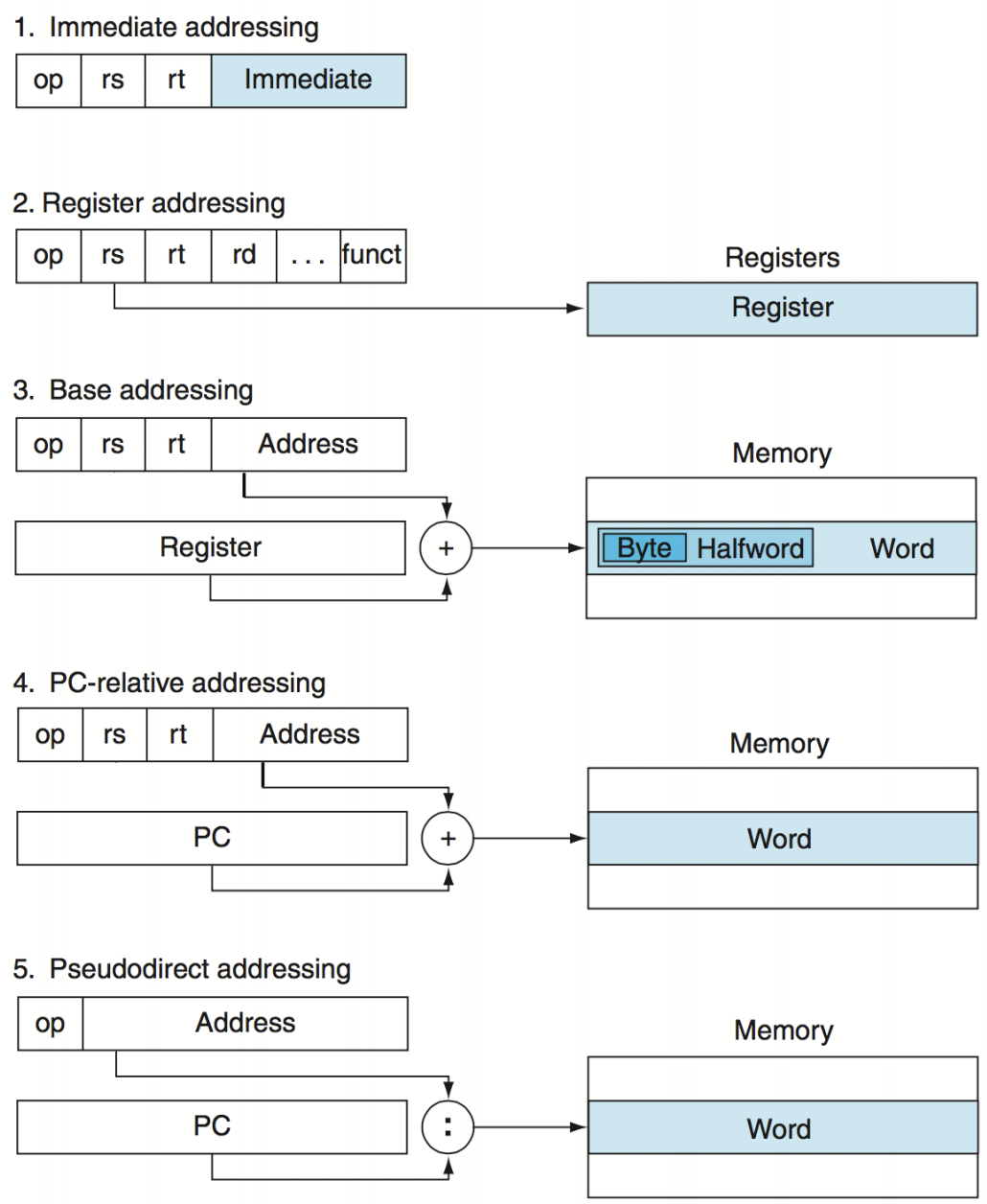
Immediate addressing : i로 끝나는 명령어들

operand는 명령어 내에 있는 상수이다.
Register addressing : R-format instructions

operand는 register이다.
Base addressing : Load/Store instructions

메모리 내용이 operand이다. 메모리의 주소는 register와 명령어 내의 상수를 더해서 구한다.
PC-relative addressing : Branch instructions

PC값과 명령어 내의 상수의 합을 더해서 구한다.
Pseudodirect addressing : Jump instructions

명령어 내의 26bit를 pc의 상위 bit들과 연접하여 점프 주소를 구한다.

Translation and Startup

ca4_8

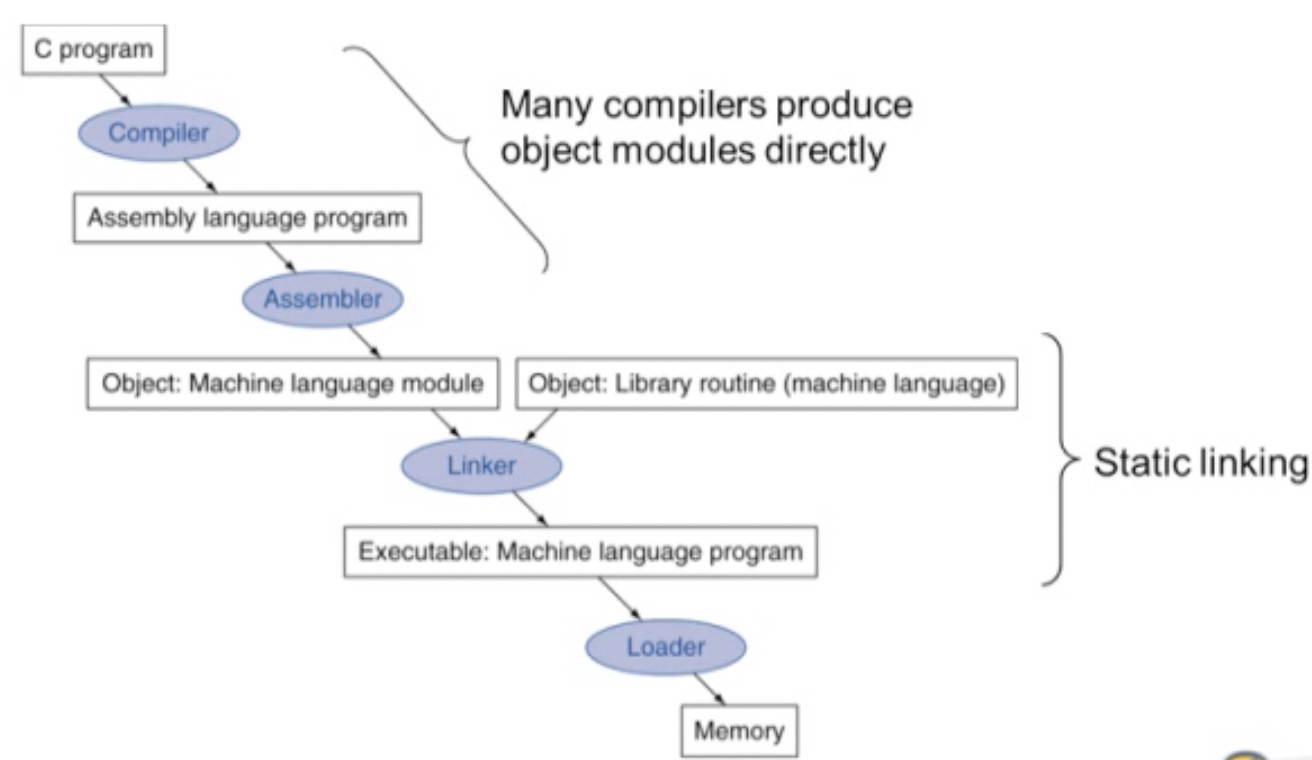
Linker : object file들을 연결해서 실행파일로 만들어 준다.
Loader : 실행 파일을 메모리에 올려서 실행시켜 준다.

Assembler Pseudoinstructions

대부분의 assembly instructions은 machine code와 일대일 표현이 된다.

Pseudoinstruction : 해당 process에서 지원해주지 않는 명령어지만 assembly 프로그래밍을 쉽게 하기 위해서 가상으로 지원해주는 명령어

# Example
# MIPS에서 지원안하는 명령어 move
move $t0, $t1
# 어셈블러를 거친 후(표현은 아래와 같이 했지만 물론 기계어이다.)
add $t0, $zero, $t1
  
# MIPS에서 지원안하는 명령어 blt(branch less than)
blt $t0, $t1, L
# 어셈블러를 거친 후
slt $at, $t0, $t1
bne $at, $zero, L

$at : assembler만 사용할 수 있는 register.

Producing an Object Module

Header : object file을 구성하는 각 부분의 크기와 위치를 나타냄.
Text segment : instructions.
Static data segment : 전역변수.
Relocation info : 시작주소에 의해서 주소가 결정되는 것들이 있다. 그런 것들에 대한 정보.
Symbol table : 함수, 전역변수에 대한 정보를 가지고 있다.
Debug info : 디버깅을 위해서 소스파일에 대한 정보를 갖고 있다.

Object file들은 위와 같은 정보들을 갖고 있다. Object file들을 하나로 연결해서 실행파일을 만들게 된다.

Linking Object Modules

object codes에서 segment를 합친다.
각각의 object code에서 사용된 Label들의 주소값을 결정해준다.
외부 및 내부 참조를 해결한다.

Location dependency들은 냅둘 수 있다. 컴퓨터에서는 대부분 virtual memory를 쓰기 때문에 program은 virtual memory공간에서 절대주소를 갖고 load되면 된다. virtual memory가 지원이 안되면 relocating loader로 Location dependent 값들을 다 바꿔줘야 한다.

Loading a Program

Header 를 읽어서 각각의 segment의 크기를 알아낸다.
virtual address space를 만든다. text와 data가 들어가야하기 때문이다.
text와 data를 메모리로 복사한다.
main에 전달해야할 argument가 있으면 Stack에 복사.
register초기화. $sp는 사용 가능한 첫 주소를 가리키게 한다.
Start-up routine으로 점프. (C에서는 main으로 점프.)

Dynamic Linking

실행할 때 linking 된다는 것.

API, Library 함수를 만들어 사용할 때 dynamic linking을 많이 사용한다. relocatable한 procedure code가 필요하다.

장점
1. 실제 이미지의 크기가 커지지 않는다.
  
  C program에 printf()를 쓰는 함수가 쓰였다고 해보자.
  - Static linking의 경우는 printf에 관련된 함수의 코드들이 내 실행파일 안으로 들어온다.
  - Dynamic linking은 printf에 관련된 함수의 코드들을 dynamic linking library file에 따로 갖고 있다. 따라서 내가 부르는 함수만큼의 크기만 필요하다.
2. 자동으로 새로운 library가 적용되게 할 수 있다.

Lazy Linkage

ca4_9

_{사진 출처}

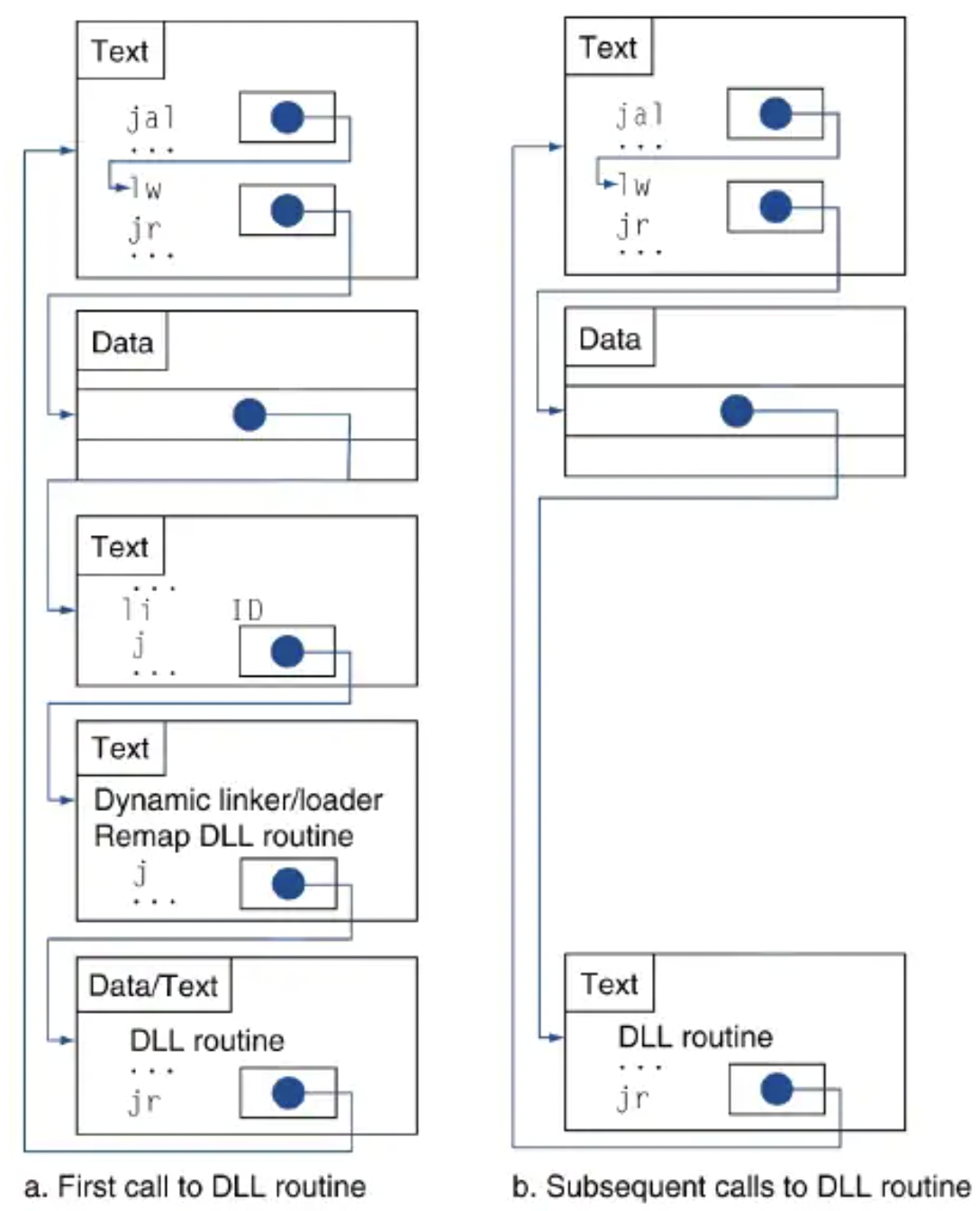
Dynamic Linking을 처음하게 되면 내가 사용한 프로그램에서 쓴 모든 라이브러리 함수에 대해서 위 그림처럼 미리 다 불러서 a->b가 되도록 작업을 해준다. 근데 예를 들어서 라이브러리에서 100개의 함수를 프로그램에서 쓴다고 가정하면, 실제로는 100개 중 10개만 자주 쓰는 경우가 있을 수 있다. 그럴 경우에 lazy linkage를 안쓰면 100개의 함수에 대해서 미리 저렇게 다 바꿔놓게 됨으로써 실행할 때 오래 걸린다. 그러나lazy linkage는 그 함수를 실행할 때만 위와 같이 바꿔줌으로써 처음 실행할 때 오래걸리지 않는다.

← → Top