on
Selection Sort
Algorithm Tag
알고리즘에 대해 공부하기 위한 태그이다.
Selection Sort(선택 정렬)
알고리즘을 처음 공부하게 됐다. 일단 가장 기본이라고 생각되는 “정렬”에 대해서 먼저 배워보자. 정수형 배열을 오름차순으로 정렬할 것이다. 동빈나 유투브를 보고 공부했다.
“가장 작은 것을 선택해서 앞으로 보내기”
일단 아이디어 자체는 위와 같다. 매우 간단하면서도 직관적이다. 우리는 오름차순 정렬을 할 것이기에 가장 작은 것을 앞으로 보내는 것. 더 정확히 말하자면, 가장 작은 숫자를 선택해서 현재 배열의 index위치 값과 ‘교환’하는 것이다.
Step by step
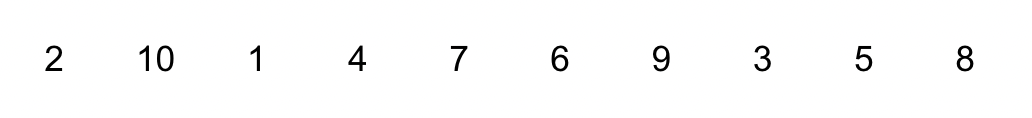
위와 같이 10개의 숫자가 나열됐다고 해보자. 우리는 이제부터 selection sort 방식으로 위 숫자들을 오름차순 정렬을 시킬 것이다.
Step 1

맨 첫 index부터 시작해서 끝까지 살펴본 다음에 가장 작은 값을 찾는다. 현재 여기에선 배열의 2번째 index인 1이 최솟값이다.
Step 2
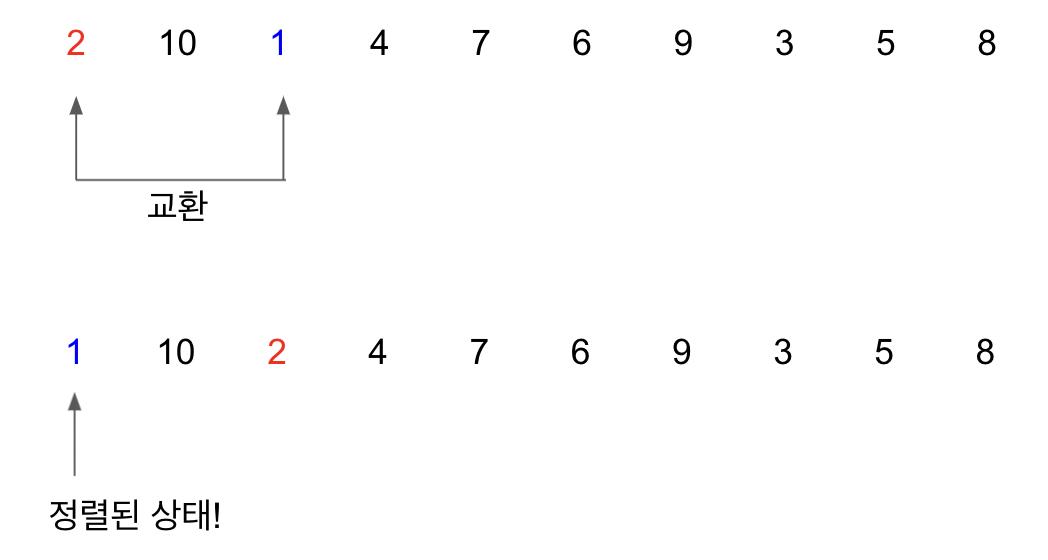
배열의 2번째 값 1 을 현재 탐색을 시작했던 위치의 값과 ‘교환’한다. 현재 1 은 탐색결과 이 배열에서 가장 작은 숫자이다. 가장작은 숫자가 맨 앞으로 갔기에 1이라는 값은 정렬된 상태라고 할 수 있다.
마찬가지로 이번에는 배열의 1번째 index의 값부터 끝까지 탐색을 하여 가장 작은 숫자를 찾은 뒤 현재 위치와 작은 숫자의 위치를 바꾸는 식으로 반복하면 된다. 현재 탐색 위치가 배열의 끝까지 갔을 때 정렬은 완료된다.
Java Code(영상 보기 전)
int[] sel = new int[SIZE]; // Selection Sort TEST
for (int i = 0; i < SIZE; i++) {
int min = sel[i];
int index = -1;
for (int j = i + 1; j < SIZE; j++) {
if (min > sel[j]) {
min = sel[j];
index = j;
}
}
if (index == -1) continue; // already sorted
int temp = sel[i];
sel[i] = sel[index];
sel[index] = temp;
}
영상을 보기 전에 위에서 말했던 “아이디어” 하나만 보고 코드를 작성해봤다.
현재 탐색을 시작한 값을 최솟값으로 정한 다음, 그 이후부터 탐색하면서 가장 작은 값을 찾으려 했다.
- 만약 현재 탐색을 시작한 값이 가장 작은 값이라면 index=-1이기에
continue를 사용하여 swap 과정을 생략했다. - 현재 탐색을 시작한 값보다 작은 값이 나오면 해당 index와 현재 값을 ‘교환’ 하도록 했다.
Answer
강의를 본 후 나의 코드와는 뭔가가 다름을 깨닳았다. (강의는 C++이므로 적당히 바꿨다)
int index = 0;
for (int i = 0; i < SIZE; i++) {
int min = 999999;
for (int j = i; j < SIZE; j++) {
if (min > sel[j]) {
min = sel[j];
index = j;
}
}
int temp = sel[i];
sel[i] = sel[index];
sel[index] = temp;
}
나의 코드와의 차이점은 비교할 최솟값을 현재 탐색 시점으로 했느냐의 차이였다.
내가 작성했던 코드에서는 현재 탐색의 위치값을 최솟값을 했기에 그 다음부터 탐색하면 됐다. 그러나 영상의 코드는 첫 최솟값을 이 배열 요소들의 값보다 무조건 큰 값을 최솟값으로 설정했기에 2번째 for문의 if문이 무조건 동작하게 되는 것이었다. 내가 작성한 코드는 그렇지 않았기에 if (index == -1) continue; 이와 같은 다른 조건을 써서 해결했었다.
Time Complexity
시간 복잡도에 대해서 알아보자. (유투브 영상의 코드를 기준으로 구했다.) 현재 10개의 요소들을 계산할 때, 맨 처음 탐색에는 10번의 비교를 했었다. 그 다음 탐색에는 9번의 비교를 했어야 했다.
첫번째 탐색 : 10번의 비교
두번째 탐색 : 9번의 비교
세번째 탐색 : 8번의 비교
...
아홉번째 탐색 : 1번의 비교
열번째 탐색 : 0번의 비교
종료.
이런식으로 비교를 한 행위가 바로 정렬하기 위한 연산이다. Selection Sort는 여기서 총 10+9+8+..2+1+0 번의 연산을 하게 되고 이를 수식으로 표현하면 (10 + 1)x10 / 2가 된다.
그렇다면 N개의 데이터에 대한 시간복잡도는 어떻게 될까? \(\text{Time Complexity}={N*(N+1)\over2}\) 가 된다.
보통 시간복잡도는 Big-O 표기법으로 나타내는데 이는 계수와 낮은 차수의 항을 제외시키는 방법이다. 따라서 Big-O 표기법에 따른 Selection Sort의 시간 복잡도는 \(\text{Selection Sort Time Complexity}=O(N^{2})\) 와 같이 된다. 만약 10000개의 값이 있었고 이를 정렬한다면, 1억번의 연산을 수행해야 하는 것이다.
Java 함수와 비교
Java에는 배열을 오름차순으로 정렬해주는 package가 있다. Arrays 라는 package를 사용해서 내가 짠 코드와 비교를 해볼 것이다.
int[] sel = new int[SIZE]; // Selection Sort TEST
int[] sys = new int[SIZE]; // System function TEST
long startTime, endTime;
// random array generate
for (int i = 0; i < SIZE; i++) {
double value = Math.random();
sel[i] = (int) (value * SIZE);
sys[i] = (int) (value * SIZE);
}
먼저 위와 같이 sel, sys 라는 정수형 배열을 만든 뒤 랜덤한 값을 넣어줬다. (sel, sys 는 같은 값을 가지는 배열이다.)
startTime = System.currentTimeMillis(); // 시간 측정을 위함
for (int i = 0; i < SIZE; i++) {
int min = sel[i];
int index = -1;
for (int j = i + 1; j < SIZE; j++) {
if (min > sel[j]) {
min = sel[j];
index = j;
}
}
if (index == -1) continue; // already sorted
int temp = sel[i];
sel[i] = sel[index];
sel[index] = temp;
}
endTime = System.currentTimeMillis();
System.out.println("Selection sort time : " + (endTime - startTime) + "ms");
아까 내가 작성했던 코드를 사용했다. 시간 측정을 위해 정렬을 시작할 때와 끝냈을 때의 시각의 차이를 계산했다.
// Java Sort
startTime = System.currentTimeMillis();
Arrays.sort(sys);
endTime = System.currentTimeMillis();
System.out.println("Java sort time : " + (endTime - startTime) + "ms");
Java의 Arrays라는 package의 내장 함수를 사용했다.
Selection sort time : 2780ms
Java sort time : 25ms
총 100000개의 데이터에 대해 위와 같은 결과를 보였다. 어마무시한 차이가 있음을 알게됐다. 결과를 보면서 알 수 있듯이 Selection Sort는 비효율적임을 알 수 있었다.