Written by xi-jjun
on October 07, 2021

Quick Sort

Algorithm Tag

알고리즘에 대해 공부하기 위한 태그이다.

Quick Sort

이름 부터 뭔가 되게 빠를 것 같다.

개념 - 우리는 오름차순 정렬을 구현하려고 한다
1. 배열의 한 원소를 선택.(이번 포스팅에서는 배열의 가운데 index의 원소를 선택할 것이다.) 이 원소를 pivot 값이라고 한다.
2. pivot보다 큰 값은 오른쪽으로, 작은 값은 왼쪽 그룹으로 정렬.
  1. pivot을 기준으로 왼쪽 그룹에서는 pivot보다 큰 값을 찾는다. 해당 값을 left로 표시.
  2. pivot을 기준으로 오른쪽 그룹에서는 pivot보다 작은 값을 찾는다. 해당 값을 right로 표시.
  3. 만약 왼쪽과 오른쪽 탐색의 위치가 엇갈리는 순간(left > right) 그 지점을 기준으로 배열을 나눈뒤 loop 종료.
  4. 만약 엇갈리지 않았다면, 2-1, 2-2에서 찾은 값을 swap. 그 후 왼쪽 탐색 위치를 +1, 오른쪽 탐색 위치를 -1.(그 다음 탐색을 위해)
3. 2-3에서 loop가 종료된 후 2그룹으로 나뉘는데 각각의 그룹에 대해서 그룹의 크기가 1이 될 때까지 1부터 재귀적 실행.

Insertion sort나 Selection sort와는 달리 글로봤을 때는 이해가 잘 안간다. 자세한 동작을 보면서 구현해보도록 하자.

Step by step

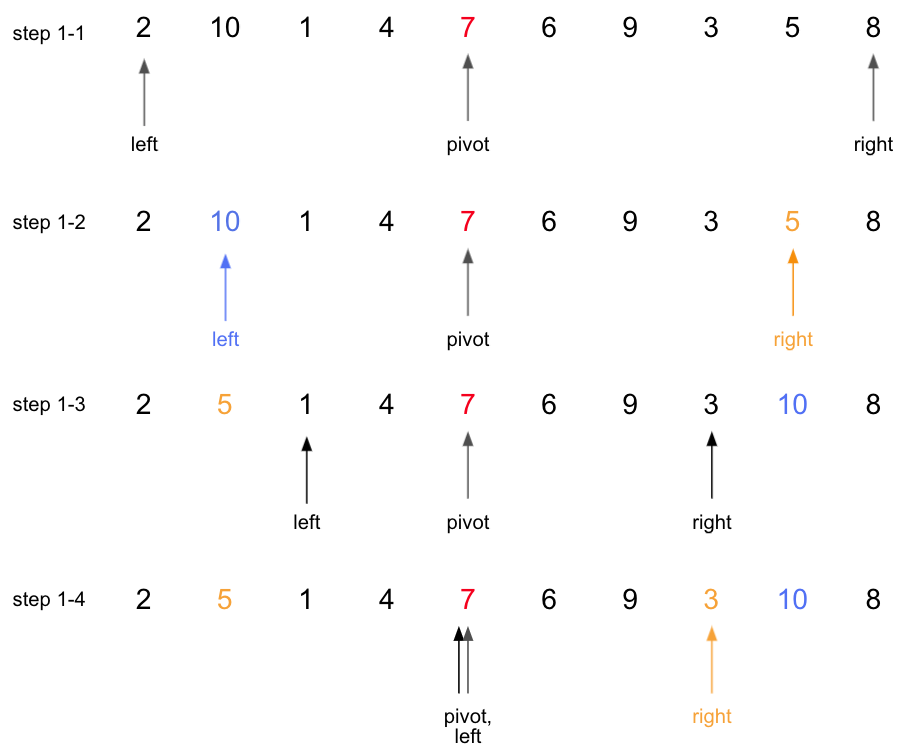
quick1

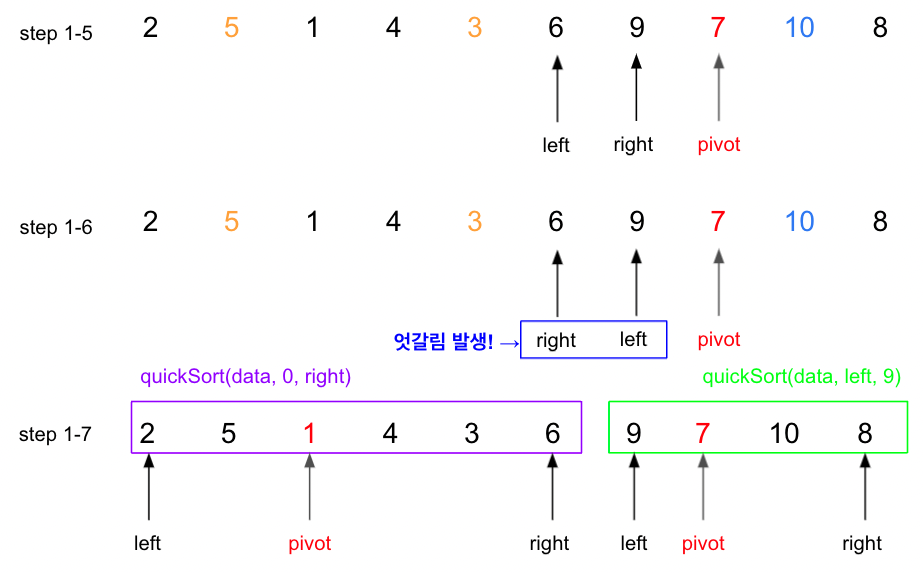
quick_re1

step1-1 : pivot=7(중앙값)이고, 왼쪽 그룹에서는 7보다 큰 값을 찾으면 left로 표시. 오른쪽 그룹에서는 7보다 작은 값을 찾으면 right표시.
step1-2 : left=1(값10의 index), right=8(값5의 index)가 됨.
step1-3 : left <= right 이므로 해당 index의 값들을 swap. 그 후 다음 탐색 위치 설정(left++(값1의 index), right--(값3의 index))
step1-4 : 왼쪽 그룹에서는 pivot(==7)보다 큰 값 없으므로 left=4(값7의 index)가 됨. 오른쪽 그룹에서는 right=7(값3의 index)가 됨.
step1-5 : pivot(==7)과 right=7(값3의 index)가 swap. 그 후 left와 right 의 다음 탐색 위치로 설정.
step1-6 : left > right 이므로 while loop 탈출.
step1-7 : 2개의 그룹으로 나뉘어 재귀적 실행.

…반복하면 된다. 반복하다가 그룹의 크기가 1이되면 right쪽 재귀 종료. 다시 돌아와서 left쪽 그룹을 정리해준다.

정렬이 되는 이유는 pivot의 왼쪽에는 무조건 pivot보다 작은 값이 오고, 오른쪽에는 무조건 pivot보다 큰 값이 온다는 것.

Time Complexity

Best case - O(N*logN)

가장 최고의 경우는 pivot의 값이 항상 ideal일 경우이다. ideal한 경우는 매 분할마다 pivot을 기준으로 왼쪽, 오른쪽 배열이 나뉘는 경우이다.

예를 들어서 31개의 원소들을 갖는 배열을 생각해보자.

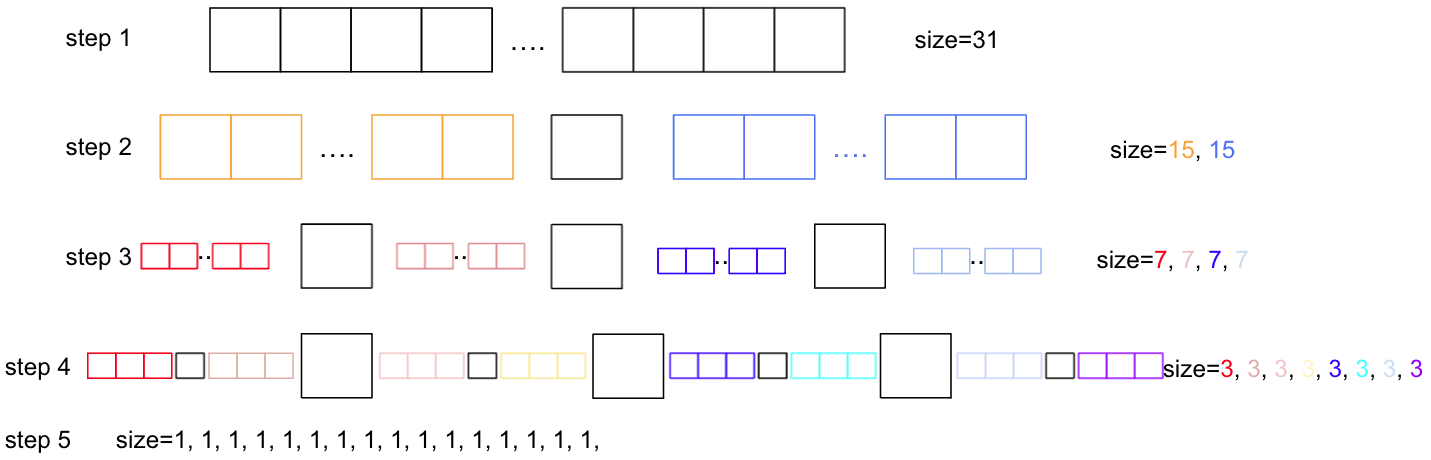
위 그림과 같이 총 4번의 분할 과정을 거치 정렬이 완료된다. 분활 횟수를 k, 원소의 개수를 n 이라고 하면, k = logn 의 식을 만족하게 된다. 원소의 개수 n만큼 비교를 진행하므로 최종적인 quick sort의 연산 횟수는 n*logn 가 된다.
Worst case - O(N*N)

pivot값이 만에 해당 그룹의 최대/최소 값일 경우 문제가 된다. 분할하여 그룹을 나눈 뒤 해당 그룹에서 정렬 알고리즘 수행이 quick sort이다. 따라서 분할되는 그룹의 수가 적을수록 유리한데, pivot의 값이 해당 그룹의 최대/최소이면 그룹이 분할될 때 크기가 1인 그룹과 나머지 원소들 그룹으로 계속 분할이 될 것이다.

따라서 이 과정을 n만 진행하게 되고, 매번 n-1개의 data들과 비교하게 된다. 결국 time complexity = O(N²)가 된다.

결론적으로 Quick sort는 O(N²)의 time complexity를 가지고(Big-O notation은 최악의 경우를 나타내기 때문), 평균적으로는 Θ(n*logn)의 time complexity를 가지게 된다.

구현

import java.io.*;
import java.util.LinkedList;

public class QuickSort {
    public static void quickSort(LinkedList<Integer> data, int l, int r) {
        int left = l; // 탐색할 부분의 왼쪽시작.
        int right = r; // 탐색할 부분의 오른쪽시작
        int pivot = data.get((l + r) / 2); // 탐색할 부분의 중간값. => 피벗값. 이 값을 기준으로 왼쪽에는 pivot보다 작은 값을 모아두고, 오른쪽에는 큰 값을 모은다.

        do {
            while (data.get(left) < pivot) left++; // 왼쪽부터 오른쪽으로 가면서 탐색. pivot 값보다 크다면 해당 index를 Left로 표시.
            while (data.get(right) > pivot) right--; // 오른쪽부터 왼쪽으로 가면서 탐색. pivot 값보다 작으면 해당 index를 Right로 표시.
            if (left <= right) { // 엇갈리지 않았다면 left와 right에 있는 값은 swap
                int temp = data.get(left); // swap...
                data.set(left, data.get(right)); // ...
                data.set(right, temp); // ...swap end
                left++; // 다음으로 탐색을 시작할 부분으로 index를 옮긴다.
                right--; // 다음으로 탐색을 시작할 부분으로 index를 옮긴다.
            }
        } while (left <= right); // 왼쪽과 오른쪽의 index가 엇갈리면 종료. pivot값을 기준으로 왼쪽 부분은 pivot보다 작고, 오른쪽 부분은 pivot값 보다 큰 수만 있게 된다.

        if (l < right) quickSort(data, l, right); // 왼쪽 index가 오른쪽탐색시작위치보다 작으면 재귀적 실행.
        if (r > left) quickSort(data, left, r); // 오른쪽 index가 왼쪽탐색시작보다 크면 재귀적 실행.
    }
}

Java의 linkedList로 구현했다.

← → Top