Hash table

Data Structure

Java언어 공부와 병행하면서 자료구조에 대해 공부할 생각이다.

Hash table

key를 value 에 mapping 할 수 있는 자료구조. - 출처

key-value pair 를 hash function으로 hash table에 mapping 하는 프로세스 또는 기술을 ‘hashing’이라고 한다. - 출처

hash function을 잘 만들수록 더욱 빠르고 효과적인 hash table을 만들 수 있다. 아래 그림을 보면 한눈에 이해하기가 더욱 쉬울 것이다.

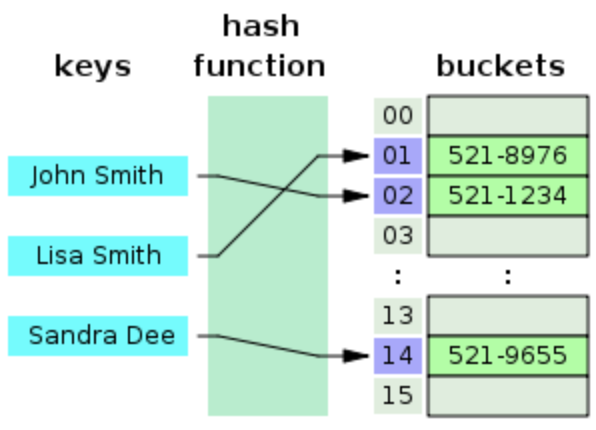
hash table 은 각각의 고유한 key 값에 hash function을 적용해 index를 만든 다음, index를 사용하여 배열에 접근한다. 여기서 중요한 것은 key로 데이터를 조회할 때 O(1)의 time complexity를 가진다는 것이다. 왜냐하면 key를 hash function에 1번만 넣으면 바로 해당 index가 나오기 때문이다.

동작

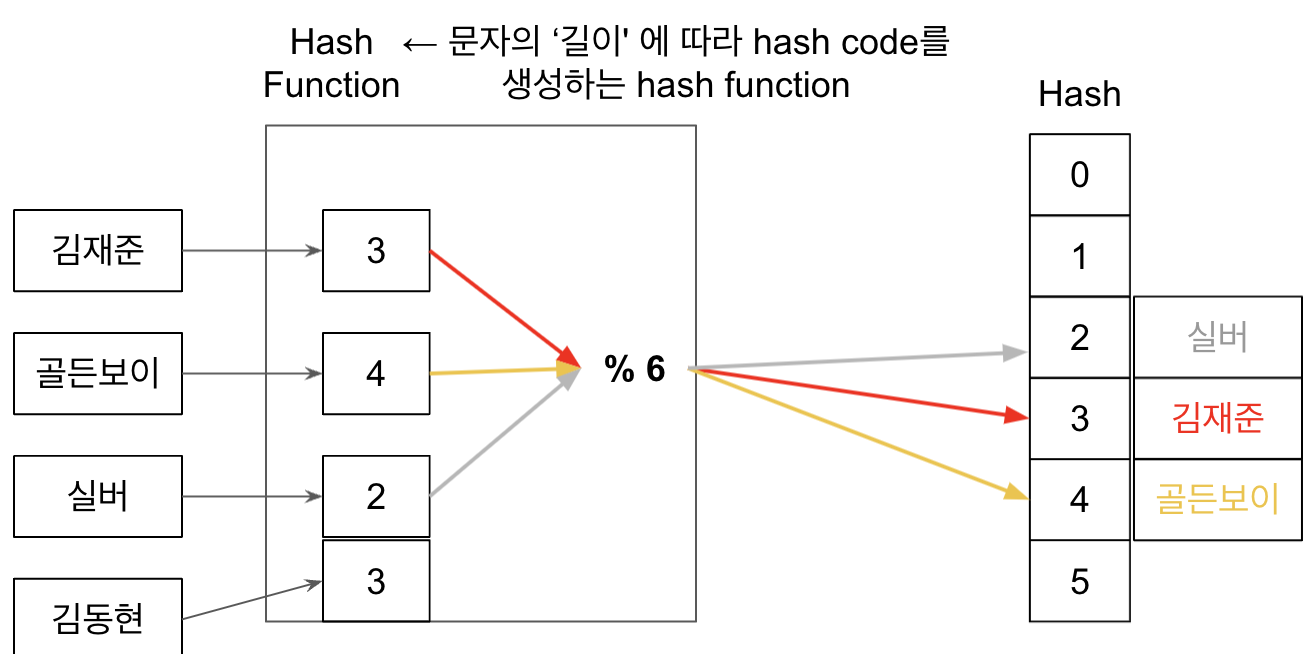
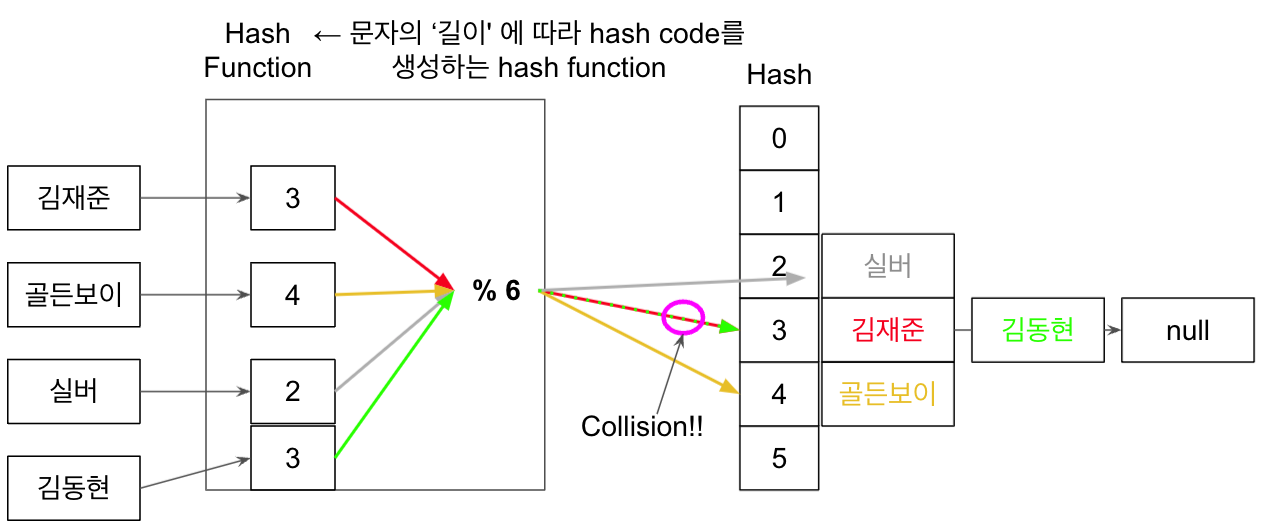
위 예시에서의 hash function은 간단하게 ‘문자열의 길이’를 기준으로 hash 배열의 크기만큼 mod 연산을 한 값을 return한다고 해보자.

김재준, 골드보이, 실버라는 3명의 이름은 각각의 고유한 hash code를 부여받아서 배열에 저장될 것이다. 그리고 나중에 hash table에 실버라는 이름을 조회하고 싶으면 hash function에 해당 key(==실버)를 넣어서 hash code(==2)라는 값을 얻어서 table에서 조회하면 된다. hash function에서의 연산 1회가 조회하는데 필요한 전부이므로 당연하게도 time complexity는 아까 위에서 말한 것처럼 O(1)가 된다.

Hash Collision

위에서 간단하게나마 예시로 hash table이 어떻게 동작하는지 알았다. 근데 그렇게 hash function을 통해 얻은 hashcode(==index)가 겹치는 경우가 생기면 어떻게 될까? 바로 충돌이 일어나게 된다. 이를 hash collision 또는 hash clash라 부른다.

2개의 서로 다른 data들이 같은 hash value, 즉 같은 hash code를 가질 때 발생한다. - 출처

아까 위에서 들었던 예시를 한번 더 보자. 하나의 key가 더 들어올려고 한다.

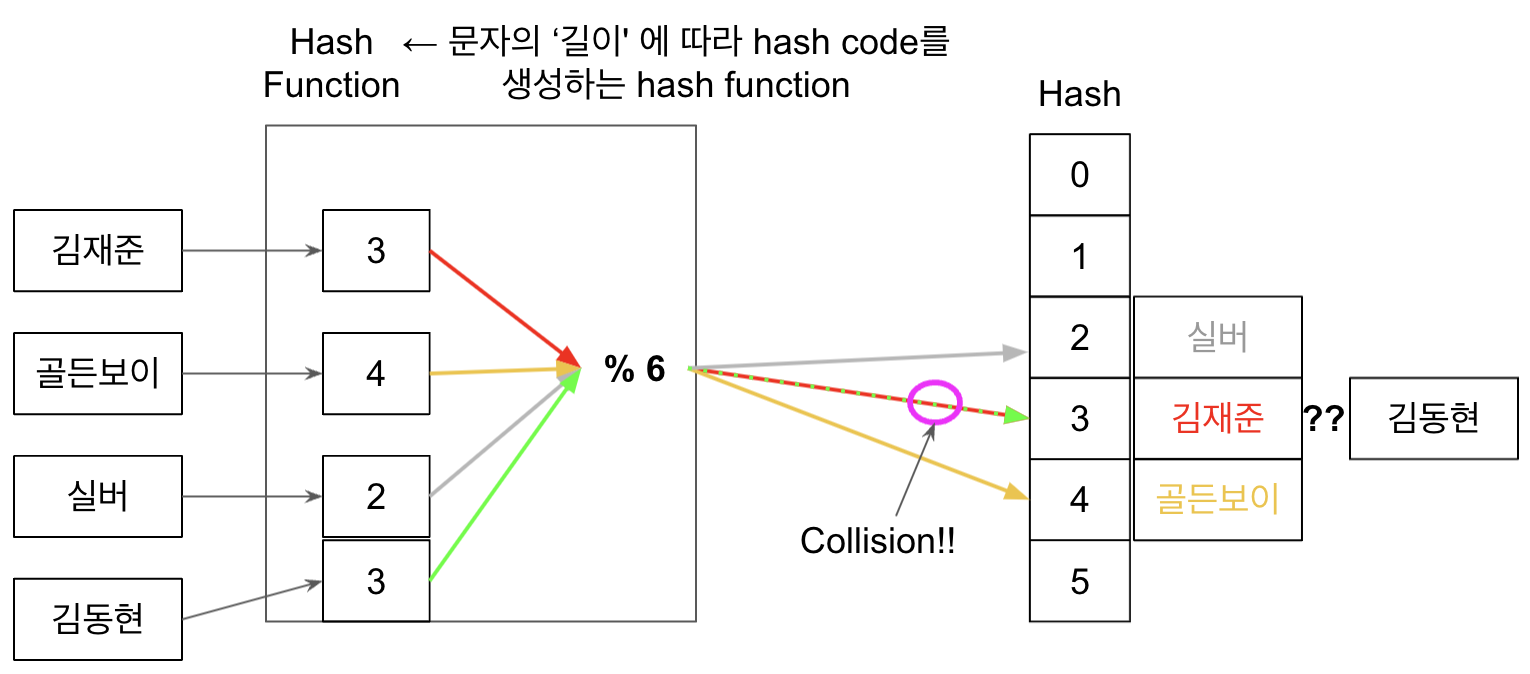
김동현이라는 이름이 hash table에 들어오려고 한다. 당연하게도 hash function을 통과해서 나온 hash code는 3…? 아까 김재준이라는 key가 받은 hash code 또한 3이었다. 배열에 저장하려고 보니깐 이미 값이 안에 있는 것이다!!

Perfect Hash Function - 해당 사이트 참고

동일하지 않은 object X, Y가 있다고 해보자. X.equals(Y)==false → X.hashcode() != Y.hashcode()이면 해당 hash function을 perfect hash function이라고 부른다. - 출처

구별되는 객체의 종류가 적다면, perfect hash 함수를 구현할 수 있겠지만 String, POJO(Plain Old Java Object) 에 대하여 perfect hash function을 구현하는 것은 불가능하다.

• Why?

  hashcode는 int data type이다. 따라서 2³² 만큼의 표현이 가능하다. 그러나 논리적으로 그보다 더 큰 객체의 수가 있다면 어쩔 수 없이 충돌은 일어날 것이다.(비둘기 집 원리)

  → 따라서 hash function을 이용하는 associative array 구현체에서는 실제 hash function의 표현 범위보다 작은 원소가 있는 배열을 사용한다.

Collision 대처 방법

충돌을 피할 수 없기에 충돌이 발생하더라도, key-value가 잘 저장되고 조회되도록 하는 대표적인 2가지 방법이 있다.

• Open Addressing : 데이터를 삽입하려는 해시 버킷이 이미 사용 중인 경우 다른 해시 버킷에 해당 데이터를 삽입하는 방식. 데이터를 저장/조회할 해시 버킷을 찾을 때에는 Linear Probing, Quadratic Probing 등의 방법을 사용
• Separate Chaining : 각 배열의 인자는 인덱스가 같은 해시 버킷을 연결한 링크드 리스트의 첫 부분(head)

Open Addressing - 참고

만약 충돌이 일어났을 때, 배열의 다른 비어있는 공간을 찾아서 해당 index에 저장하는 것.

Hash code(==index)에 대한 충돌 처리에서 LinkedList와 같은 추가적인 메모리 공간을 사용하는 것이 아니라 배열 내 다른 공간을 사용하는 것.

• Linear probing

  index에 대해 충돌이 발생했을 때 index 뒤에 있는 버킷중에 빈 버킷을 찾아서 데이타를 넣는 방식.

  

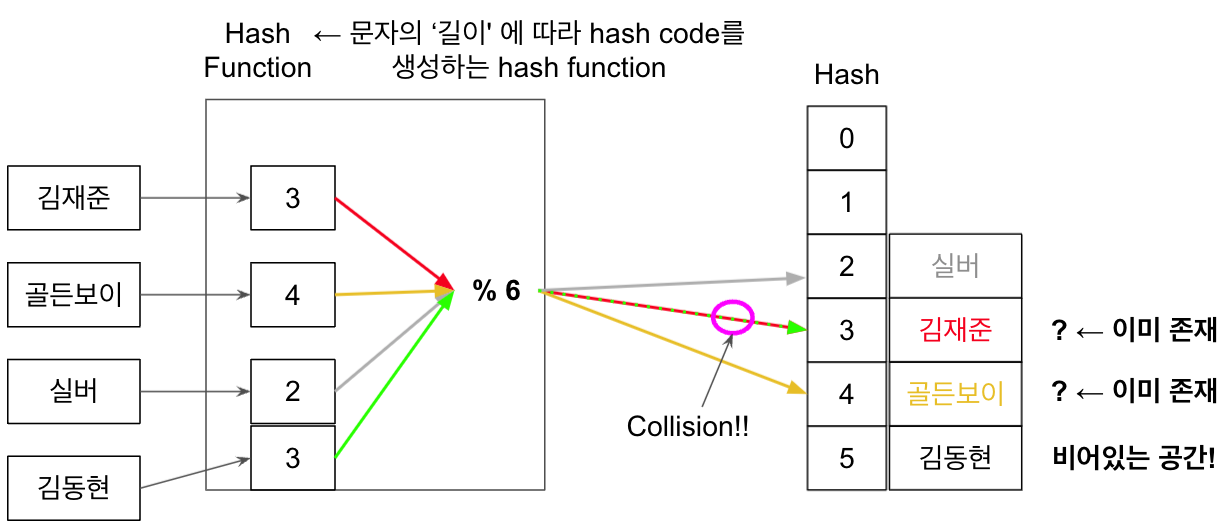
  김동현은 index(==3)이지만, 이미 김재준이라는 key가 존재한다. 따라서 배열의 다음 index를 탐색했으나 골드보이 존재. 그 다음 index 탐색했을 때 빈 공간이 나오므로 해당 index에 저장.

  → primary clustering(특정 지역에 원소가 몰리는 현상)에 취약.

• Quadratice probing - 출처

  index에 대해 충돌이 발생하면 i번째 index에서 i²th index가 빈 공간인지 탐색한다.

  • 동작 - index x에서 충돌이 일어난 상황
    1. If the slot hash(x) % S is full, then we try (hash(x) + 1*1) % S.
    2. If (hash(x) + 1*1) % S is also full, then we try (hash(x) + 2*2) % S.
    3. If (hash(x) + 2*2) % S is also full, then we try (hash(x) + 3*3) % S…
    4. 빈 공간 찾을 때까지 반복.

  → secondary clustering에 취약.

• Double hashing

  말 그대로 2개의 hash function을 사용. 위 2개의 문제점은 clustering. 원소가 몰리는 현상이 발생하여 성능의 저하를 일으키는 것이었다. (결국엔 init hash code가 같다면, 탐색하게 되는 index들도 같기 때문) 따라서 2개의 hash function을 사용하여 같은 init hashcode 에 대하여 clustering을 방지하게 된다.

  h_i = (h(x) + i*f(x)) mod m 이라는 식으로 표현할 수 있다. (h와 f가 hash function)

Separate Chaining

Chaining : 같은 hash code로 들어오는 모든 원소들을 하나의 LinkedList로 관리한다.

이와 같이 같은 hash code에 대하여 LinkedList로 원소들을 이어준다.

Java HashMap

위의 두 방법은 모두 조회할 때 worst case O(M)이다. 즉, 내가 hash table에 저장한 M개의 원소들이 모두 1개의 hash code를 가질 때 이므로 조회를 하기 위해선 하나하나 살펴보는 수밖에 없다.

Java에서는 Separate Chaining방식을 사용한다. open addressing 방식은 데이터의 삭제에 있어서 비효율적이게 되고, M의 개수가 커짐에 따라서 open addressing의 캐시 적중률이 낮아지기 때문에 캐시 효율이 낮아지게 되기 때문이다. 자세한 내용은 여기를 확인바란다.

Java8의 HashMap에서 해시 함수 값이 균등 분포(uniform distribution) 상태라고 할 때, get(key) method 호출에 대한 기댓값은 log(N/M)을 보장한다.

→ 왜냐하면 같은 hash code의 요소들을 LinkedList가 아닌 tree라는 자료구조를 사용했기 때문이다. 자료가 더욱 많아진다면, N/M 과 log(N/M)의 차이는 무시할 수 없을만큼 커지게 된다.

그렇다면 과연 LinkedList와 Tree 중 어느 것을 사용하게 될까? 라는 생각이 들 수 있다. 그에 대한 답변도 해당 사이트에 설명이 돼있다.

링크드 리스트를 사용할 것인가 트리를 사용할 것인가에 대한 기준은 하나의 해시 버킷에 할당된 키-값 쌍의 개수이다. 하나의 해시 버킷에 8개의 키-값 쌍이 모이면 링크드 리스트를 트리로 변경한다. 만약 해당 버킷에 있는 데이터를 삭제하여 개수가 6개에 이르면 다시 링크드 리스트로 변경한다…

결론

오늘은 간략하게나마 hash table에 대해서 알아봤다. 해당 사이트를 가장 많이 참고해서 글을 적었고, 그렇기에 이 블로그 글을 읽는 것보다는 사이트 가서 읽는 것을 추천한다. 더 자세한 내용이 쉽고 간단하게 설명돼있다. 구현 자체는 생략하였다. 구현을 잘 하는 것보단 이론을 이해하는게 더 중요하다고 생각해서이다.

결국엔 hash code가 고르게 분포되는 hash function을 갖는게 중요하다는 것을 배웠다. (사이트에는 ‘최근의 해시 함수는 균등 분포가 잘 되게 만들어지는 경향이 많아’라고 언급이 됐다…)