on
Floyd-Warshall
Algorithm Tag
알고리즘에 대해 공부하기 위한 태그이다.
Floyd Warshall Algorithm
변의 가중치가 음이거나 양인 가중 그래프에서 최단 경로를 찾는 알고리즘. - 출처
오늘 백준 문제를 풀다가 어떤 문제를 오늘 보게 됐는데 아이디어가 떠오르지 않는 것이었다! 그래서 자존심이 상하지만 문제의 알고리즘 유형을 살펴보니 Floyd-Warshall이라고 적혀 있었다.
따라서 오늘 포스팅은 Floyd-Warshall 알고리즘이다.
핵심 아이디어
‘거쳐가는 정점’을 기준으로 최단 거리를 구하는 것. - 출처
Wikipedia에서 어려운 수학 기호를 보는 것 보다 직접 예시를 보면서 천천히 알고리즘을 따라해보는게 더 이해가 잘 갔다. 예시를 보도록 하자.
-
아래 그림과 같은 그래프가 있다. 먼저 해당 그래프를 인접행렬로 나타내보자. 그래프는 무방향+가중치가 1로 동일하다.
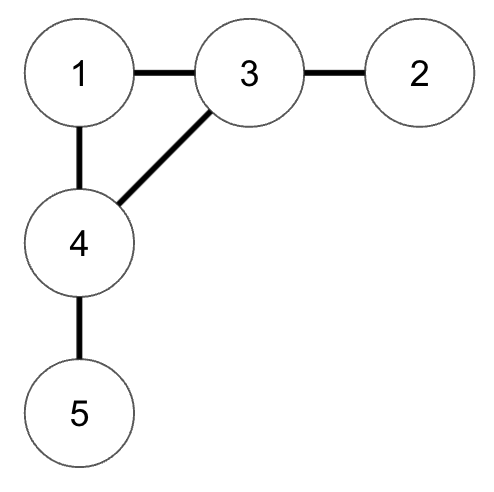
그래프
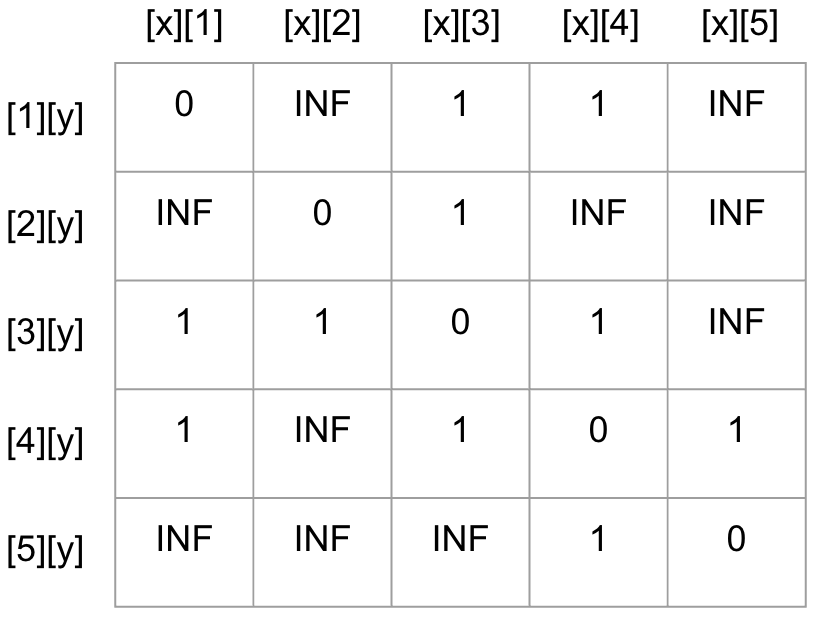
그래프를 인접 행렬로 표현
2번째 그림의 인접행렬 표를 한번 보자. 먼저, 행 또는 열 index가 0인 경우는 나타내지 않았음을 알길 바란다.
[start][end]: start→end 로 바로가는 길이 있다면 해당 길의 ‘가중치(비용)’ 를 행렬의 값으로 넣어준다.[1][1]: 1→1로 가는 경우는 자기자신에게 돌아온다는 의미다. 따라서 가만히 있으면 되므로 0. 나머지start==end인 경우도 마찬가지로 0이 된다.[1][2]: 1→2로 가는 경우. 그래프를 보면 바로 연결돼있지 않다. 따라서 무한대의 가중치를 가진다고 하여INF로 표현.[1][3]: 1→3로 가는 경우. 1 오른쪽에 3이 있다. 연결돼있고, 현재 그래프의 가중치는 1이므로1이라는 값을 넣어준다.
마찬가지로 나머지 경우도 위와 같이 해주면 인접행렬을 만들 수 있다.
-
위 테이블이 의미하는 바는 현재까지 계산된 최소 비용이다. 우리는 여기서 모든 정점에 대하여 경유하는 정점을 비교하여 최소비용을 구할 것이다.
-
1번 정점을 거쳐가는 경우
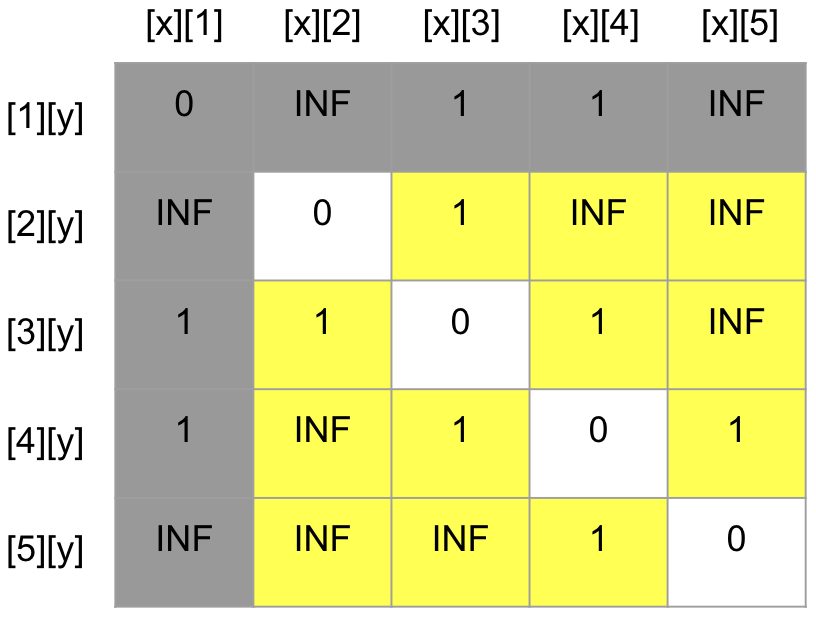
노란색으로 칠한 영역만 업데이트 해주면 된다.
[2][3]: 현재 값은 2→3의 비용1이 저장돼있다. 우리는 현재 1번 정점을 경유하는 경우와 비교하는 중이므로[2][3]을[2][1]->[1][3]과 같이 생각해준 뒤에 비용(가중치)를 구할 것이다.[2][1]→[1][3]: INF + 1 =INF[2][1]: 2→1인 경우의 비용.INF[1][3]: 1→3인 경우의 비용.1
원래 비용이
1. 1번 정점을 경유하는 경우의 비용은INF. 최소비용을 구하는 것이기에1값을 넣어준다. 나머지 경우도 위와 비슷하게 해서 테이블을 업데이트 하면 된다. -
내가 든 예시는 2번 정점까지는 테이블의 변화가 없으므로 바로 3번 정점을 경유하는 경우를 보도록 해보자.
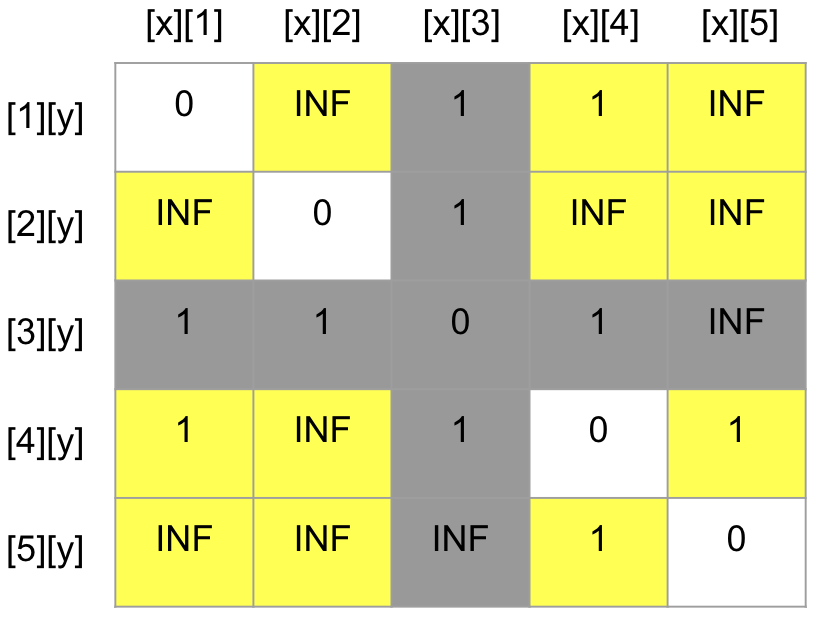
[1][2]: 원래 비용은INF이지만, 3번 정점을 경유하게 되면 2의 비용으로 갈 수 있게 된다는 사실을 알 수 있다.[1][3]→[3][2]: 1 + 1 =2의 비용을 갖게 된다.
[1][4]: 원래 비용은1이었고, 3번 정점을 경유하게 되면 2의 비용으로 가게 된다. 따라서 원래 비용 유지.[1][3]→[3][4]: 1 + 1 =2의 비용을 갖게 된다.
나머지 정점에 대해서도 이렇게 테이블을 업데이트 해주면서 최소비용을 구해주면 된다.
-
결과
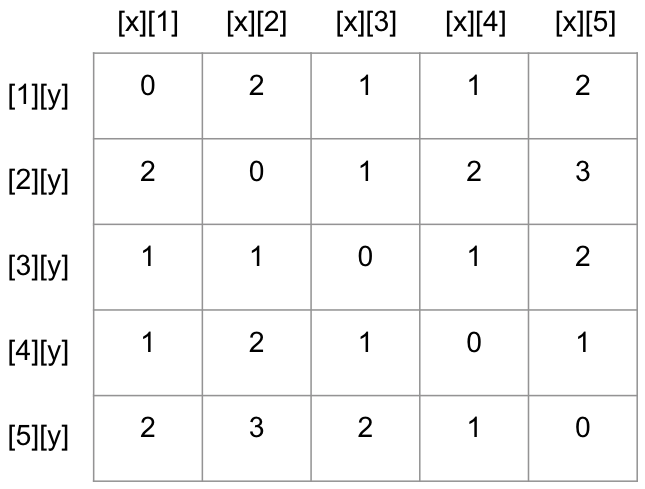
테이블을 완성하게 되면 위와 같이 된다.
소스 코드
static void floyd(int[][] graph) { // time complexity O(N^3)
for (int k = 1; k < N + 1; k++) {
for (int i = 1; i < N + 1; i++) {
for (int j = 1; j < N + 1; j++) {
if (i == j) continue;
graph[i][j] = Math.min(graph[i][j], graph[i][k] + graph[k][j]);
}
}
}
}
하나의 경유 정점 k에 대하여 모든 정점을 순회해야 하므로 3중 for문이 만들어 진다. 따라서 자연스럽게 시간 복잡도는 O(N3)가 된다.
백준 문제 풀이
해당 문제에 대한 풀이를 진행해보자.
풀이의 방향은
- 한 정점에서 다른 정점으로 가는 최소비용들을 구한다.
- 해당 값을 다 더한다.
- 나머지 정점들에 대해서도 1~2 단계에서 더한 값을 구해준 뒤, 가장 작은 값의 정점을 답으로 출력한다. 이 때, 합이 가장 작은 값이 여러개라면 숫자가 더 작은 정점을 출력한다.
난 1번을 어떻게 해야할지 몰랐었다. 하지만 이제는 알기에 자신있게 코드를 작성할 수 있었다.
Java source code
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
// baekJoon 1389 silver1 케빈 베이컨의 6단계 법칙
// Floyd-Warshall https://chanhuiseok.github.io/posts/algo-50/ 참고
public class S1389 {
static final int INF = 100000000; // 문제 조건보다 큰 값이기에 무한의 역할로서 충분한 크기.
static int N, M;
static void floyd(int[][] graph) { // time complexity O(N^3)
for (int k = 1; k < N + 1; k++) {
for (int i = 1; i < N + 1; i++) {
for (int j = 1; j < N + 1; j++) {
if (i == j) continue;
graph[i][j] = Math.min(graph[i][j], graph[i][k] + graph[k][j]);
}
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken()); // user number
M = Integer.parseInt(st.nextToken()); // relation
int[][] graph = new int[N + 1][N + 1];
reset(graph);
while (M-- > 0) {
st = new StringTokenizer(br.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
graph[A][B] = 1;
graph[B][A] = 1;
}
floyd(graph);
int min = 10000000;
int minIdx = 0;
for (int i = 1; i < N + 1; i++) {
int sum = 0;
for (int j = 1; j < N + 1; j++) {
if (i == j) continue;
sum += graph[i][j];
}
if (min > sum) {
minIdx = i;
min = sum;
}
}
System.out.println(minIdx);
}
private static void reset(int[][] graph) {
for (int i = 1; i < N + 1; i++) {
for (int j = 1; j < N + 1; j++) {
if (i == j) continue;
graph[i][j] = INF;
}
}
}
}